Thursday maths with Lesley- thinking hats needed

 

Thursday challenge 1.

If we double each side of a small square we get a new enlarged square:

The new enlarged square is the size of four of the smaller squares.

This also happens when we enlarge other shapes. Some, like the squares, can be filled with the same smaller shape.

Look at these:



Can you work out how the four shapes fit to make the enlarged shape each time?
You need to rotate or reflect the smaller shapes to fit them in. (This means that if you make them from squared paper you will need to turn them round or turn them over.)

Thursday challenge 2. 

We have 5 cubes and we're going to put them together, following a few simple rules:

• the cubes must be together face-to-face;

• they must not be toppling over.

We're going to paint the faces that can be seen.  One Brush Load (a kind of unit that we'll use) will paint one square face.

Challenge 
Can you find ways of arranging 5 cubes so that:

• you need as few BLs (Brushloads) as possible?
• you need as many BLs as possible?

Need more information about counting BLs before you start the challenge?
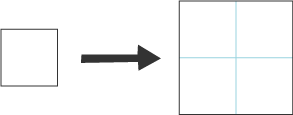
Here are 5 cubes:



Counting the faces to be painted comes to 15, so 15 Brush Loads are needed.  (Remember we're only counting visible faces, so not those that are touching the surface where the cubes are placed.)

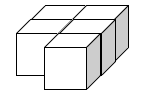
But of course we could have placed the 5 cubes differently, for example:



Counting the faces to be painted now, we have 17, so 17  Brush Loads.

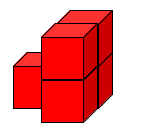
And, how about:



Now we'll need 21  Brush Loads (BLs).

Going further
Can you find arrangements that need all the numbers between the largest and the smallest numbers of BLs?

Take more cubes.......
What happens if you use more cubes, for example 6, 7, 8 ...? 
Can you find out the smallest number of BLs and the largest number of BLs possible in each case? 

Can you predict the arrangements which need as few BLs as possible and as many BLs as possible?